---

Here, we would like to provide definitions of different types of convergence and discuss how they are related. Consider a sequence of random variables $X_1$, $X_2$, $X_3$, $\cdots$, i.e, $\big\{X_n, n \in \mathbb{N}\}$. This sequence might ''converge'' to a random variable $X$. There are four types of convergence that we will discuss in this section:

1. Convergence in distribution,
2. Convergence in probability,
3. Convergence in mean,
4. Almost sure convergence.

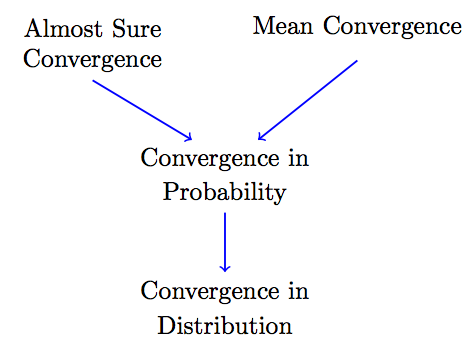
These are all different kinds of convergence. A sequence might converge in one sense but not another. Some of these convergence types are ''stronger'' than others and some are ''weaker.'' By this, we mean the following: If Type A convergence is stronger than Type B convergence, it means that Type A convergence implies Type B convergence. Figure 7.4 summarizes how these types of convergence are related. In this figure, the stronger types of convergence are on top and, as we move to the bottom, the convergence becomes weaker. For example, using the figure, we conclude that if a sequence of random variables converges in probability to a random variable $X$, then the sequence converges in distribution to $X$ as well.

---