7.2.2 Sequence of Random Variables
Here, we would like to discuss what we precisely mean by a sequence of random variables. Remember that, in any probability model, we have a sample space $S$ and a probability measure $P$. For simplicity, suppose that our sample space consists of a finite number of elements, i.e.,
\begin{align}%\label{} S=\{s_1,s_2,\cdots, s_k\}. \end{align} Then, a random variable $X$ is a mapping that assigns a real number to any of the possible outcomes $s_i$, $i=1,2, \cdots, k$. Thus, we may write \begin{align}%\label{} X(s_i)=x_i, \qquad \textrm{ for }i=1,2,\cdots, k. \end{align}When we have a sequence of random variables $X_1$, $X_2$, $X_3$, $\cdots$, it is also useful to remember that we have an underlying sample space $S$. In particular, each $X_n$ is a function from $S$ to real numbers. Thus, we may write
\begin{align}%\label{} X_n(s_i)=x_{{\large ni}}, \qquad \textrm{ for }i=1,2,\cdots, k. \end{align} In sum, a sequence of random variables is in fact a sequence of functions $X_n:S\rightarrow \mathbb{R}$.Example
Consider the following random experiment: A fair coin is tossed once. Here, the sample space has only two elements $S=\{H,T\}$. We define a sequence of random variables $X_1$, $X_2$, $X_3$, $\cdots$ on this sample space as follows:
\begin{equation} \nonumber X_n(s) = \left\{ \begin{array}{l l} \frac{1}{n+1} & \qquad \textrm{ if }s=H \\ & \qquad \\ 1 & \qquad \textrm{ if }s=T \end{array} \right. \end{equation}- Are the $X_i$'s independent?
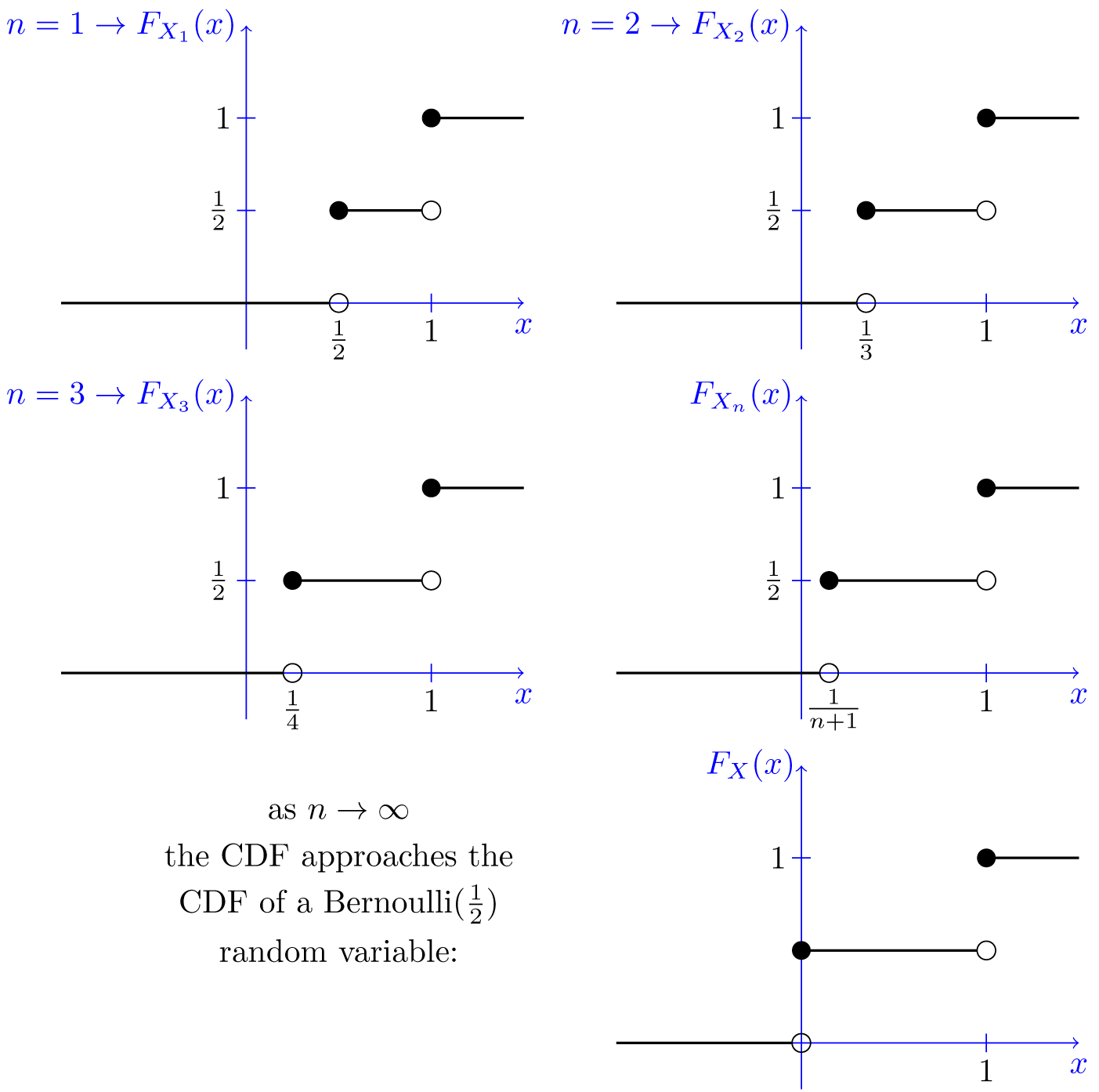
- Find the PMF and CDF of $X_n$, $F_{{\large X_n}}(x)$ for $n=1,2,3, \cdots$.
- As $n$ goes to infinity, what does $F_{{\large X_n}}(x)$ look like?
- Solution
-
- The $X_i$'s are not independent because their values are determined by the same coin toss. In particular, to show that $X_1$ and $X_2$ are not independent, we can write \begin{align}%\label{} P(X_1=1, X_2=1) &=P(T) \\ &=\frac{1}{2}, \end{align} which is different from \begin{align}%\label{} P(X_1=1)\cdot P(X_2=1) &=P(T)\cdot P(T) \\ &=\frac{1}{4}. \end{align}
- Each $X_i$ can take only two possible values that are equally likely. Thus, the PMF of $X_n$ is given by \begin{equation} \nonumber P_{{\large X_n}}(x)=P(X_n=x) = \left\{ \begin{array}{l l} \frac{1}{2} & \qquad \textrm{ if }x=\frac{1}{n+1} \\ & \qquad \\ \frac{1}{2} & \qquad \textrm{ if }x=1 \end{array} \right. \end{equation} From this we can obtain the CDF of $X_n$ \begin{equation} \nonumber F_{{\large X_n}}(x)=P(X_n \leq x) = \left\{ \begin{array}{l l} 1 & \qquad \textrm{ if }x \geq 1\\ & \qquad \\ \frac{1}{2} & \qquad \textrm{ if }\frac{1}{n+1} \leq x <1 \\ & \qquad \\ 0 & \qquad \textrm{ if }x< \frac{1}{n+1} \end{array} \right. \end{equation}
- Figure 7.3 shows the CDF of $X_n$ for different values of $n$. We see in the figure that the CDF of $X_n$ approaches the CDF of a $Bernoulli\left(\frac{1}{2}\right)$ random variable as $n \rightarrow \infty$. As we will discuss in the next sections, this means that the sequence $X_1$, $X_2$, $X_3$, $\cdots$ converges in distribution to a $Bernoulli\left(\frac{1}{2}\right)$ random variable as $n \rightarrow \infty$.
-
The previous example was defined on a very simple sample space $S=\{H,T\}$. Let us look at an example that is defined on a more interesting sample space.
Example
Consider the following random experiment: A fair coin is tossed repeatedly forever. Here, the sample space $S$ consists of all possible sequences of heads and tails. We define the sequence of random variables $X_1$, $X_2$, $X_3$, $\cdots$ as follows:
\begin{equation} \nonumber X_n = \left\{ \begin{array}{l l} 0 & \qquad \textrm{ if the $n$th coin toss results in a heads} \\ & \qquad \\ 1 & \qquad \textrm{ if the $n$th coin toss results in a tails} \end{array} \right. \end{equation} In this example, the $X_i$'s are independent because each $X_i$ is a result of a different coin toss. In fact, the $X_i$'s are i.i.d. $Bernoulli\left(\frac{1}{2}\right)$ random variables. Thus, when we would like to refer to such a sequence, we usually say, ''Let $X_1$, $X_2$, $X_3$, $\cdots$ be a sequence of i.i.d. $Bernoulli\left(\frac{1}{2}\right)$ random variables.'' We usually do not state the sample space because it is implied that the sample space $S$ consists of all possible sequences of heads and tails.
