7.1.2 Central Limit Theorem
The central limit theorem (CLT) is one of the most important results in probability theory. It states that, under certain conditions, the sum of a large number of random variables is approximately normal. Here, we state a version of the CLT that applies to i.i.d. random variables. Suppose that $X_1$, $X_2$ , ... , $X_{\large n}$ are i.i.d. random variables with expected values $EX_{\large i}=\mu < \infty$ and variance $\mathrm{Var}(X_{\large i})=\sigma^2 < \infty$. Then as we saw above, the sample mean $\overline{X}={\large\frac{X_1+X_2+...+X_n}{n}}$ has mean $E\overline{X}=\mu$ and variance $\mathrm{Var}(\overline{X})={\large \frac{\sigma^2}{n}}$. Thus, the normalized random variable
\begin{align}%\label{} Z_{\large n}=\frac{\overline{X}-\mu}{ \sigma / \sqrt{n}}=\frac{X_1+X_2+...+X_{\large n}-n\mu}{\sqrt{n} \sigma} \end{align} has mean $EZ_{\large n}=0$ and variance $\mathrm{Var}(Z_{\large n})=1$. The central limit theorem states that the CDF of $Z_{\large n}$ converges to the standard normal CDF.
The Central Limit Theorem (CLT)
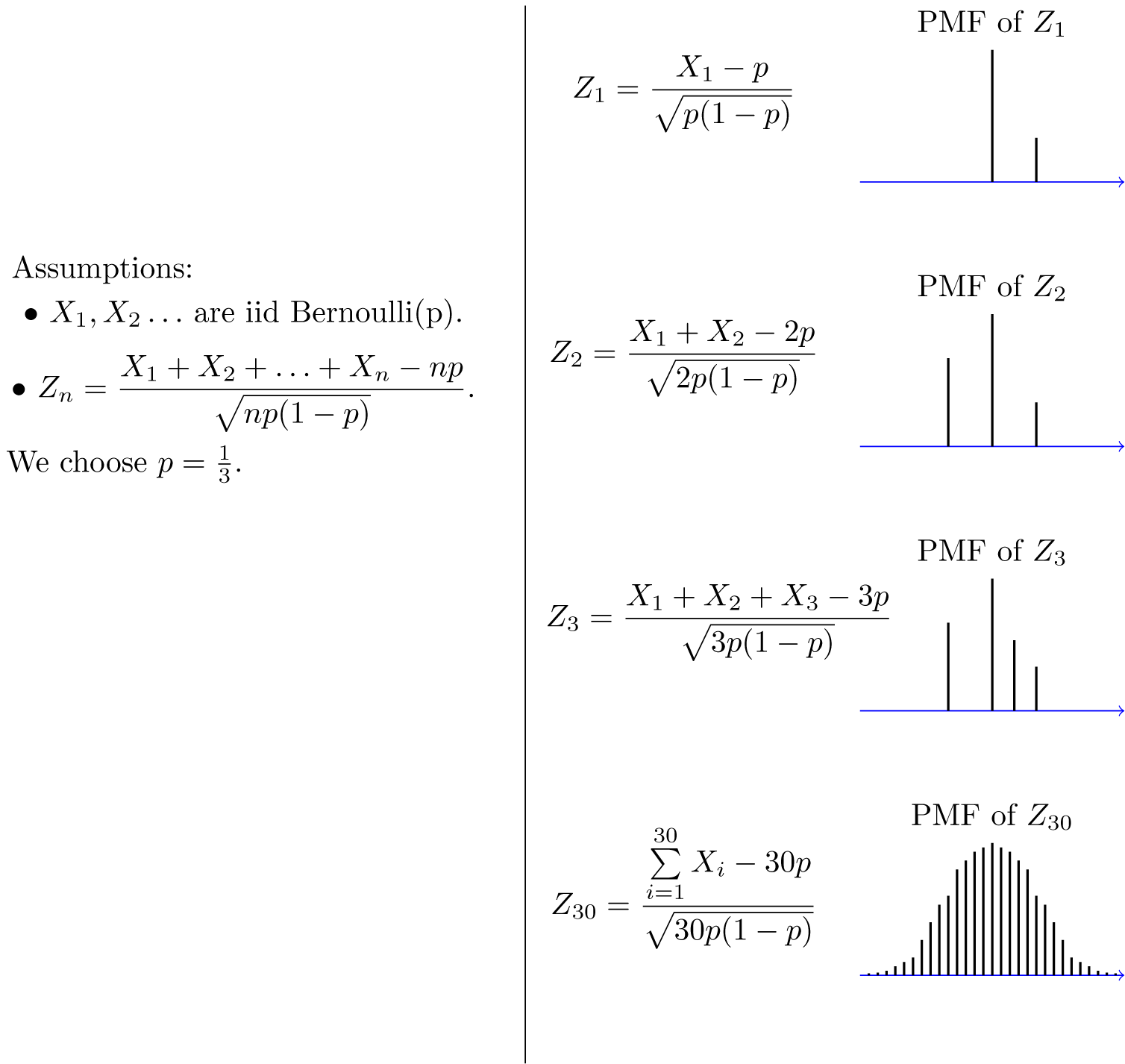
Let $X_1$,$X_2$,...,$X_{\large n}$ be i.i.d. random variables with expected value $EX_{\large i}=\mu <\infty$ and variance $0<\mathrm{Var}(X_{\large i})=\sigma^2 < \infty$. Then, the random variable \begin{align}%\label{} Z_{\large n}=\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}=\frac{X_1+X_2+...+X_{\large n}-n\mu}{\sqrt{n} \sigma} \end{align} converges in distribution to the standard normal random variable as $n$ goes to infinity, that is \begin{align}%\label{} \lim_{n \rightarrow \infty} P(Z_{\large n} \leq x)=\Phi(x), \qquad \textrm{ for all }x \in \mathbb{R}, \end{align} where $\Phi(x)$ is the standard normal CDF.An interesting thing about the CLT is that it does not matter what the distribution of the $X_{\large i}$'s is. The $X_{\large i}$'s can be discrete, continuous, or mixed random variables. To get a feeling for the CLT, let us look at some examples. Let's assume that $X_{\large i}$'s are $Bernoulli(p)$. Then $EX_{\large i}=p$, $\mathrm{Var}(X_{\large i})=p(1-p)$. Also, $Y_{\large n}=X_1+X_2+...+X_{\large n}$ has $Binomial(n,p)$ distribution. Thus,
\begin{align}%\label{}
Z_{\large n}=\frac{Y_{\large n}-np}{\sqrt{n p(1-p)}},
\end{align}
where $Y_{\large n} \sim Binomial(n,p)$. Figure 7.1 shows the PMF of $Z_{\large n}$ for different values of $n$. As you see, the shape of the PMF gets closer to a normal PDF curve as $n$ increases. Here, $Z_{\large n}$ is a discrete random variable, so mathematically speaking it has a PMF not a PDF. That is why the CLT states that the CDF (not the PDF) of $Z_{\large n}$ converges to the standard normal CDF. Nevertheless, since PMF and PDF are conceptually similar, the figure is useful in visualizing the convergence to normal distribution.
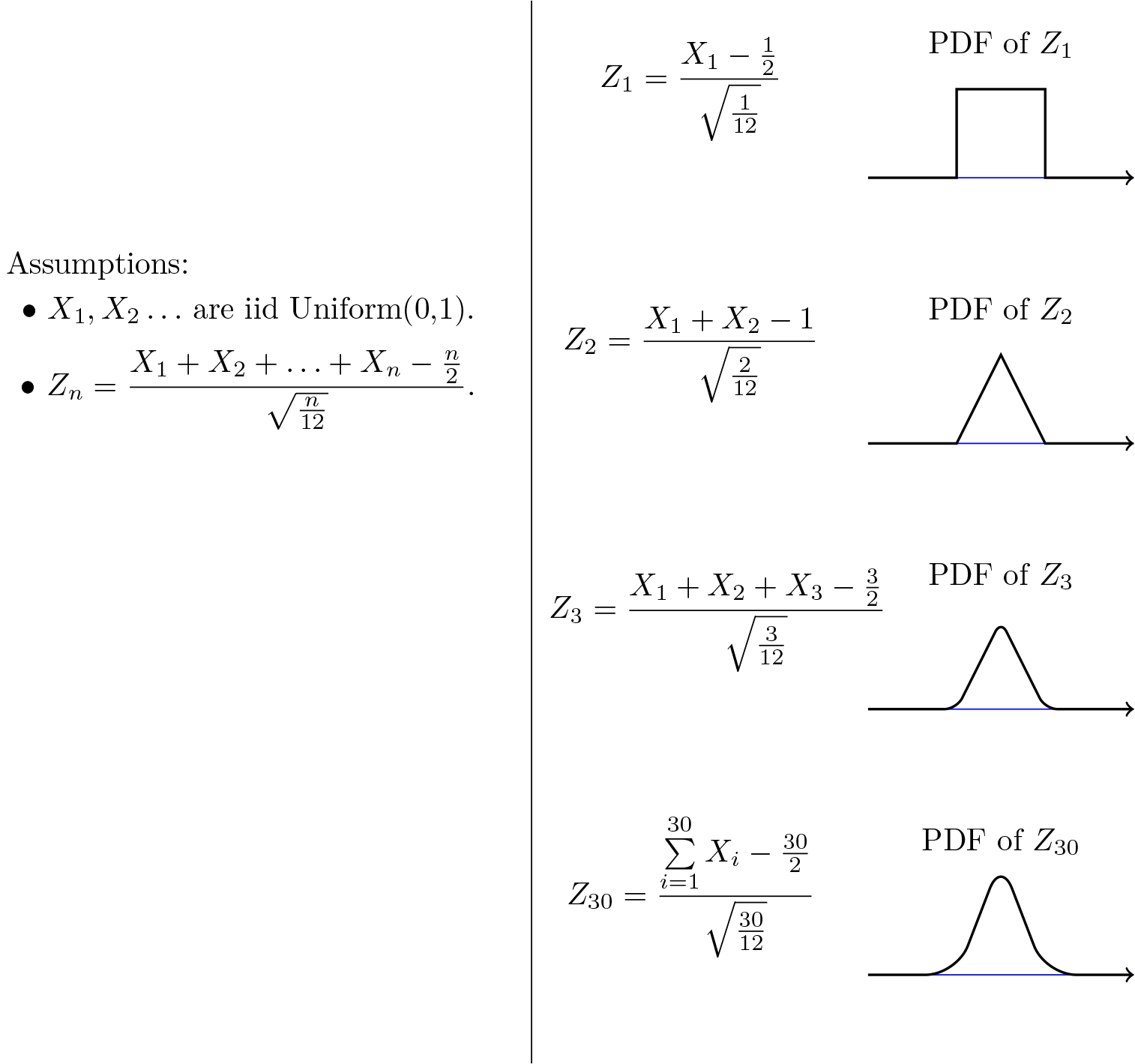
As another example, let's assume that $X_{\large i}$'s are $Uniform(0,1)$. Then $EX_{\large i}=\frac{1}{2}$, $\mathrm{Var}(X_{\large i})=\frac{1}{12}$. In this case, \begin{align}%\label{} Z_n=\frac{X_1+X_2+...+X_n-\frac{n}{2}}{\sqrt{n/12}}. \end{align} Figure 7.2 shows the PDF of $Z_{\large n}$ for different values of $n$. As you see, the shape of the PDF gets closer to the normal PDF as $n$ increases.
We could have directly looked at $Y_{\large n}=X_1+X_2+...+X_{\large n}$, so why do we normalize it first and say that the normalized version ($Z_{\large n}$) becomes approximately normal? This is because $EY_{\large n}=n EX_{\large i}$ and $\mathrm{Var}(Y_{\large n})=n \sigma^2$ go to infinity as $n$ goes to infinity. We normalize $Y_{\large n}$ in order to have a finite mean and variance ($EZ_{\large n}=0$, $\mathrm{Var}(Z_{\large n})=1$). Nevertheless, for any fixed $n$, the CDF of $Z_{\large n}$ is obtained by scaling and shifting the CDF of $Y_{\large n}$. Thus, the two CDFs have similar shapes.
The importance of the central limit theorem stems from the fact that, in many real applications, a certain random variable of interest is a sum of a large number of independent random variables. In these situations, we are often able to use the CLT to justify using the normal distribution. Examples of such random variables are found in almost every discipline. Here are a few:
-
Laboratory measurement errors are usually modeled by normal random variables.
In communication and signal processing, Gaussian noise is the most frequently used model for noise.
-
In finance, the percentage changes in the prices of some assets are sometimes modeled by normal random variables.
-
When we do random sampling from a population to obtain statistical knowledge about the population, we often model the resulting quantity as a normal random variable.
The CLT is also very useful in the sense that it can simplify our computations significantly. If you have a problem in which you are interested in a sum of one thousand i.i.d. random variables, it might be extremely difficult, if not impossible, to find the distribution of the sum by direct calculation. Using the CLT we can immediately write the distribution, if we know the mean and variance of the $X_{\large i}$'s.
Another question that comes to mind is how large $n$ should be so that we can use the normal approximation. The answer generally depends on the distribution of the $X_{\large i}$s. Nevertheless, as a rule of thumb it is often stated that if $n$ is larger than or equal to $30$, then the normal approximation is very good.
Let's summarize how we use the CLT to solve problems:
How to Apply The Central Limit Theorem (CLT)
Here are the steps that we need in order to apply the CLT:- Write the random variable of interest, $Y$, as the sum of $n$ i.i.d. random variable $X_{\large i}$'s: \begin{align}%\label{} Y=X_1+X_2+...+X_{\large n}. \end{align}
- Find $EY$ and $\mathrm{Var}(Y)$ by noting that \begin{align}%\label{} EY=n\mu, \qquad \mathrm{Var}(Y)=n\sigma^2, \end{align} where $\mu=EX_{\large i}$ and $\sigma^2=\mathrm{Var}(X_{\large i})$.
- According to the CLT, conclude that $\frac{Y-EY}{\sqrt{\mathrm{Var}(Y)}}=\frac{Y-n \mu}{\sqrt{n} \sigma}$ is approximately standard normal; thus, to find $P(y_1 \leq Y \leq y_2)$, we can write \begin{align}%\label{} P(y_1 \leq Y \leq y_2) &= P\left(\frac{y_1-n \mu}{\sqrt{n} \sigma} \leq \frac{Y-n \mu}{\sqrt{n} \sigma} \leq \frac{y_2-n \mu}{\sqrt{n} \sigma}\right)\\ &\approx \Phi\left(\frac{y_2-n \mu}{\sqrt{n}\sigma}\right)-\Phi\left(\frac{y_1-n \mu}{\sqrt{n} \sigma}\right). \end{align}
Let us look at some examples to see how we can use the central limit theorem.
Example
A bank teller serves customers standing in the queue one by one. Suppose that the service time $X_{\large i}$ for customer $i$ has mean $EX_{\large i} = 2$ (minutes) and $\mathrm{Var}(X_{\large i}) = 1$. We assume that service times for different bank customers are independent. Let $Y$ be the total time the bank teller spends serving $50$ customers. Find $P(90 < Y < 110)$.
- Solution
-
\begin{align}%\label{} Y=X_1+X_2+...+X_{\large n}, \end{align} where $n=50$, $EX_{\large i}=\mu=2$, and $\mathrm{Var}(X_{\large i})=\sigma^2=1$. Thus, we can write \begin{align}%\label{} P(90 < Y \leq 110) &= P\left(\frac{90-n \mu}{\sqrt{n} \sigma}<\frac{Y-n \mu}{\sqrt{n} \sigma}<\frac{110-n \mu}{\sqrt{n} \sigma}\right)\\ &=P\left(\frac{90-100}{\sqrt{50}}<\frac{Y-n \mu}{\sqrt{n} \sigma}<\frac{110-100}{\sqrt{50}}\right)\\ &=P\left(-\sqrt{2}<\frac{Y-n \mu}{\sqrt{n} \sigma}<\sqrt{2}\right). \end{align} By the CLT, $\frac{Y-n \mu}{\sqrt{n} \sigma}$ is approximately standard normal, so we can write \begin{align}%\label{} P(90 < Y \leq 110) &\approx \Phi(\sqrt{2})-\Phi(-\sqrt{2})\\ &=0.8427 \end{align}
-
Example
In a communication system each data packet consists of $1000$ bits. Due to the noise, each bit may be received in error with probability $0.1$. It is assumed bit errors occur independently. Find the probability that there are more than $120$ errors in a certain data packet.
- Solution
-
Let us define $X_{\large i}$ as the indicator random variable for the $i$th bit in the packet. That is, $X_{\large i}=1$ if the $i$th bit is received in error, and $X_{\large i}=0$ otherwise. Then the $X_{\large i}$'s are i.i.d. and $X_{\large i} \sim Bernoulli(p=0.1)$. If $Y$ is the total number of bit errors in the packet, we have
\begin{align}%\label{} Y=X_1+X_2+...+X_{\large n}. \end{align} Since $X_{\large i} \sim Bernoulli(p=0.1)$, we have \begin{align}%\label{} EX_{\large i}=\mu=p=0.1, \qquad \mathrm{Var}(X_{\large i})=\sigma^2=p(1-p)=0.09 \end{align} Using the CLT, we have \begin{align}%\label{} P(Y>120) &=P\left(\frac{Y-n \mu}{\sqrt{n} \sigma}>\frac{120-n \mu}{\sqrt{n} \sigma}\right)\\ &=P\left(\frac{Y-n \mu}{\sqrt{n} \sigma}>\frac{120-100}{\sqrt{90}}\right)\\ &\approx 1-\Phi\left(\frac{20}{\sqrt{90}}\right)\\ &=0.0175 \end{align}
-
Continuity Correction:
Let us assume that $Y \sim Binomial(n=20,p=\frac{1}{2})$, and suppose that we are interested in $P(8 \leq Y \leq 10)$. We know that a $Binomial(n=20,p=\frac{1}{2})$ can be written as the sum of $n$ i.i.d. $Bernoulli(p)$ random variables:
\begin{align}%\label{} Y=X_1+X_2+...+X_{\large n}. \end{align} Since $X_{\large i} \sim Bernoulli(p=\frac{1}{2})$, we have \begin{align}%\label{} EX_{\large i}=\mu=p=\frac{1}{2}, \qquad \mathrm{Var}(X_{\large i})=\sigma^2=p(1-p)=\frac{1}{4}. \end{align}
Thus, we may want to apply the CLT to write
\begin{align}%\label{} P(8 \leq Y \leq 10) &= P\left (\frac{8-n \mu}{\sqrt{n} \sigma}<\frac{Y-n \mu}{\sqrt{n} \sigma}<\frac{10-n \mu}{\sqrt{n} \sigma}\right)\\ &=P\left (\frac{8-10}{\sqrt{5}}<\frac{Y-n \mu}{\sqrt{n} \sigma}<\frac{10-10}{\sqrt{5}}\right)\\ &\approx \Phi(0)-\Phi\left (\frac{-2}{\sqrt{5}}\right)\\ &=0.3145 \end{align}Since, here, $n=20$ is relatively small, we can actually find $P(8 \leq Y \leq 10)$ accurately. We have
\begin{align}%\label{} P(8 \leq Y \leq 10) &=\sum_{k=8}^{10}{n \choose k} p^k(1-p)^{n-k}\\ &=\bigg[{20 \choose 8}+{20 \choose 9}+{20 \choose 10}\bigg] \bigg(\frac{1}{2}\bigg)^{20}\\ &= 0.4565 \end{align}We notice that our approximation is not so good. Part of the error is due to the fact that $Y$ is a discrete random variable and we are using a continuous distribution to find $P(8 \leq Y \leq 10)$. Here is a trick to get a better approximation, called continuity correction. Since $Y$ can only take integer values, we can write
\begin{align}%\label{} P(8 \leq Y \leq 10) &= P(7.5 < Y < 10.5)\\ &=P\left (\frac{7.5-n \mu}{\sqrt{n} \sigma}<\frac{Y-n \mu}{\sqrt{n} \sigma}<\frac{10.5-n \mu}{\sqrt{n} \sigma}\right)\\ &=P\left (\frac{7.5-10}{\sqrt{5}}<\frac{Y-n \mu}{\sqrt{n} \sigma}<\frac{10.5-10}{\sqrt{5}}\right)\\ &\approx \Phi\left (\frac{0.5}{\sqrt{5}}\right)-\Phi\left (\frac{-2.5}{\sqrt{5}}\right)\\ &=0.4567 \end{align}
As we see, using continuity correction, our approximation improved significantly. The continuity correction is particularly useful when we would like to find $P(y_1 \leq Y \leq y_2)$, where $Y$ is binomial and $y_1$ and $y_2$ are close to each other.
Continuity Correction for Discrete Random Variables
Let $X_1$,$X_2$, $\cdots$,$X_{\large n}$ be independent discrete random variables and let
\begin{align}%\label{} Y=X_1+X_2+\cdots+X_{\large n}. \end{align} Suppose that we are interested in finding $P(A)=P(l \leq Y \leq u)$ using the CLT, where $l$ and $u$ are integers. Since $Y$ is an integer-valued random variable, we can write \begin{align}%\label{} P(A)=P(l-\frac{1}{2} \leq Y \leq u+\frac{1}{2}). \end{align}
It turns out that the above expression sometimes provides a better approximation for $P(A)$ when applying the CLT. This is called the continuity correction and it is particularly useful when $X_{\large i}$'s are Bernoulli (i.e., $Y$ is binomial).

