3.2.1 Cumulative Distribution Function
The PMF is one way to describe the distribution of a discrete random variable. As we will see later on, PMF cannot be defined for continuous random variables. The cumulative distribution function (CDF) of a random variable is another method to describe the distribution of random variables. The advantage of the CDF is that it can be defined for any kind of random variable (discrete, continuous, and mixed).
The cumulative distribution function (CDF) of random variable $X$ is defined as $$F_X(x) = P(X \leq x), \textrm{ for all }x \in \mathbb{R}.$$
Note that the subscript $X$ indicates that this is the CDF of the random variable $X$. Also, note that the CDF is defined for all $x \in \mathbb{R}$. Let us look at an example.
Example
I toss a coin twice. Let $X$ be the number of observed heads. Find the CDF of $X$.
- Solution
-
Note that here $X \sim Binomial (2, \frac{1}{2})$. The range of $X$ is $R_X=\{0,1,2\}$ and
its PMF is given by
$$P_X(0)=P(X=0)=\frac{1}{4},$$
$$P_X(1) =P(X=1)=\frac{1}{2},$$
$$P_X(2)=P(X=2)=\frac{1}{4}.$$
To find the CDF, we argue as follows. First, note that if $x < 0$, then
$$F_X(x)=P(X \leq x)=0, \textrm{ for } x < 0.$$
Next, if $x\geq 2$,
$$F_X(x)=P(X \leq x)=1, \textrm{ for } x\geq 2.$$
Next, if $0 \leq x < 1$,
$$F_X(x)=P(X \leq x)=P(X=0)=\frac{1}{4}, \textrm{ for } 0 \leq x < 1.$$
Finally, if $1 \leq x < 2$,
$$F_X(x)=P(X \leq x)=P(X=0)+P(X=1)=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}, \textrm{ for } 1 \leq x < 2.$$
Thus, to summarize, we have
\begin{equation}
\nonumber F_X(x) = \left\{
\begin{array}{l l}
0 & \quad \text{for } x < 0\\
\frac{1}{4} & \quad \text{for } 0 \leq x < 1\\
\frac{3}{4} & \quad \text{for } 1 \leq x < 2 \\
1 & \quad \text{for } x \geq 2\\
\end{array} \right.
\end{equation}
Note that when you are asked to find the CDF of a random variable, you need to find the function for the entire real line. Also, for discrete random variables, we must be careful when to use "$ < $" or "$\leq$". Figure 3.3 shows the graph of $F_X(x)$. Note that the CDF is flat between the points in $R_X$ and jumps at each value in the range. The size of the jump at each point is equal to the probability at that point. For, example, at point $x=1$, the CDF jumps from $\frac{1}{4}$ to $\frac{3}{4}$. The size of the jump here is $\frac{3}{4}-\frac{1}{4}=\frac{1}{2}$ which is equal to $P_X(1)$. Also, note that the open and closed circles at point $x=1$ indicate that $F_X(1)=\frac{3}{4}$ and not $\frac{1}{4}$.

Fig.3.3 - CDF for Example 3.9.
-
Note that here $X \sim Binomial (2, \frac{1}{2})$. The range of $X$ is $R_X=\{0,1,2\}$ and
its PMF is given by
$$P_X(0)=P(X=0)=\frac{1}{4},$$
$$P_X(1) =P(X=1)=\frac{1}{2},$$
$$P_X(2)=P(X=2)=\frac{1}{4}.$$
To find the CDF, we argue as follows. First, note that if $x < 0$, then
$$F_X(x)=P(X \leq x)=0, \textrm{ for } x < 0.$$
Next, if $x\geq 2$,
$$F_X(x)=P(X \leq x)=1, \textrm{ for } x\geq 2.$$
Next, if $0 \leq x < 1$,
$$F_X(x)=P(X \leq x)=P(X=0)=\frac{1}{4}, \textrm{ for } 0 \leq x < 1.$$
Finally, if $1 \leq x < 2$,
$$F_X(x)=P(X \leq x)=P(X=0)+P(X=1)=\frac{1}{4}+\frac{1}{2}=\frac{3}{4}, \textrm{ for } 1 \leq x < 2.$$
Thus, to summarize, we have
\begin{equation}
\nonumber F_X(x) = \left\{
\begin{array}{l l}
0 & \quad \text{for } x < 0\\
\frac{1}{4} & \quad \text{for } 0 \leq x < 1\\
\frac{3}{4} & \quad \text{for } 1 \leq x < 2 \\
1 & \quad \text{for } x \geq 2\\
\end{array} \right.
\end{equation}
In general, let $X$ be a discrete random variable with range $R_X=\{x_1,x_2,x_3,...\}$, such that $x_1 < x_2 < x_3 < ...$ Here, for simplicity, we assume that the range $R_X$ is bounded from below, i.e., $x_1$ is the smallest value in $R_X$. If this is not the case then $F_X(x)$ approaches zero as $x \rightarrow -\infty$ rather than hitting zero. Figure 3.4 shows the general form of the CDF, $F_X(x)$, for such a random variable. We see that the CDF is in the form of a staircase. In particular, note that the CDF starts at $0$; i.e.,$F_X(-\infty)=0$. Then, it jumps at each point in the range. In particular, the CDF stays flat between $x_k$ and $x_{k+1}$, so we can write $$F_X(x)=F_X(x_k), \textrm{ for }x_k \leq x < x_{k+1}.$$
The CDF jumps at each $x_k$. In particular, we can write $$F_X(x_k)-F_X(x_k-\epsilon)=P_X(x_k), \textrm{ For $\epsilon>0$ small enough.}$$ Thus, the CDF is always a non-decreasing function, i.e., if $y \geq x$ then $F_X(y)\geq F_X(x)$. Finally, the CDF approaches $1$ as $x$ becomes large. We can write $$\lim_{x \rightarrow \infty} F_X(x)=1.$$
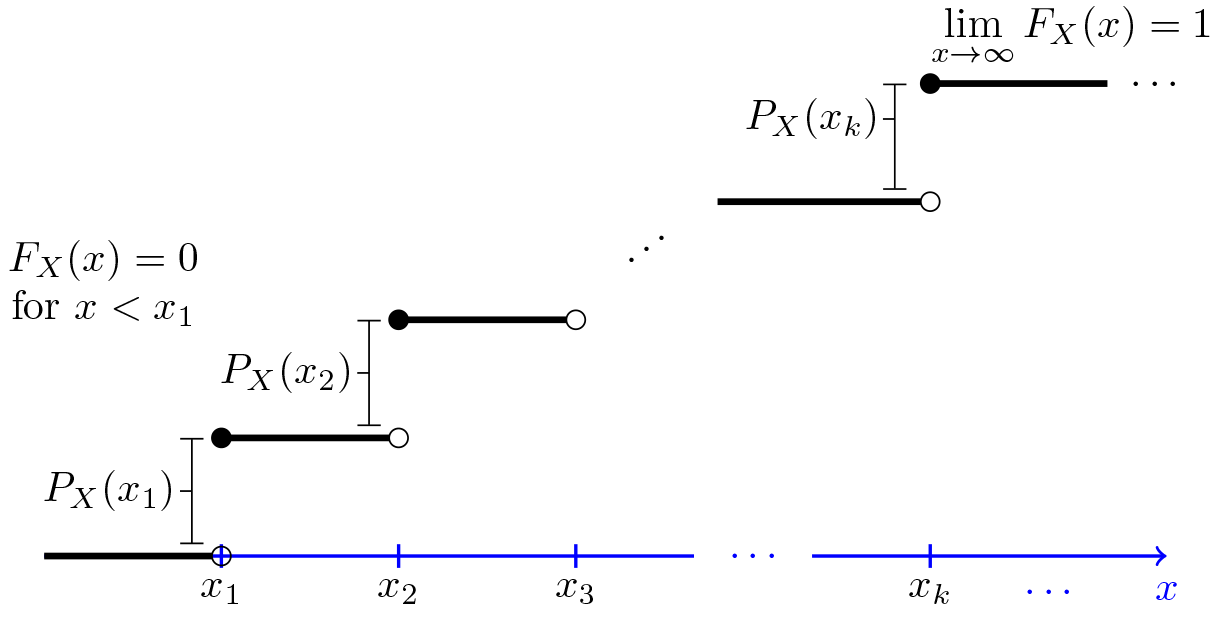
Note that the CDF completely describes the distribution of a discrete random variable. In particular, we can find the PMF values by looking at the values of the jumps in the CDF function. Also, if we have the PMF, we can find the CDF from it. In particular, if $R_X=\{x_1,x_2,x_3,...\}$, we can write $$F_X(x)=\sum_{x_k \leq x} P_X(x_k).$$ Now, let us prove a useful formula.
To see this, note that for $a \leq b$ we have $$P(X \leq b)=P(X \leq a) + P(a < X \leq b).$$ Thus, $$F_X(b)=F_X(a) + P(a < X \leq b).$$ Again, pay attention to the use of "$ < $" and "$\leq$" as they could make a difference in the case of discrete random variables. We will see later that Equation 3.1 is true for all types of random variables (discrete, continuous, and mixed). Note that the CDF gives us $P(X \leq x)$. To find $P(X < x)$, for a discrete random variable, we can simply write $$P(X < x)=P(X \leq x)-P(X=x)=F_X(x)-P_X(x).$$
Example
Let $X$ be a discrete random variable with range $R_X=\{1,2,3,...\}$. Suppose the PMF of $X$ is given by $$P_X(k)=\frac{1}{2^k} \textrm{ for } k=1,2,3,...$$
- Find and plot the CDF of $X$, $F_X(x)$.
- Find $P(2 < X \leq 5)$.
- Find $P(X > 4)$.
- Solution
-
First, note that this is a valid PMF. In particular,
$$\sum_{k=1}^{\infty} P_X(k)=\sum_{k=1}^{\infty} \frac{1}{2^k}=1 \textrm{ (geometric sum)}$$
- To find the CDF, note that
$\textrm{For } x < 1,$ $F_X(x)=0$. $\textrm{For } 1\leq x < 2,$ $F_X(x)=P_X(1)=\frac{1}{2}$. $\textrm{For } 2\leq x < 3,$ $F_X(x)=P_X(1)+P_X(2)=\frac{1}{2}+ \frac{1}{4}=\frac{3}{4}$.
In general we have $$\textrm{For } 0 < k \leq x < k+1,$$ $$F_X(x) =P_X(1)+P_X(2)+...+P_X(k)$$ $$=\frac{1}{2}+ \frac{1}{4}+...+\frac{1}{2^k}=\frac{2^k-1}{2^k}.$$Figure 3.5 shows the CDF of $X$.
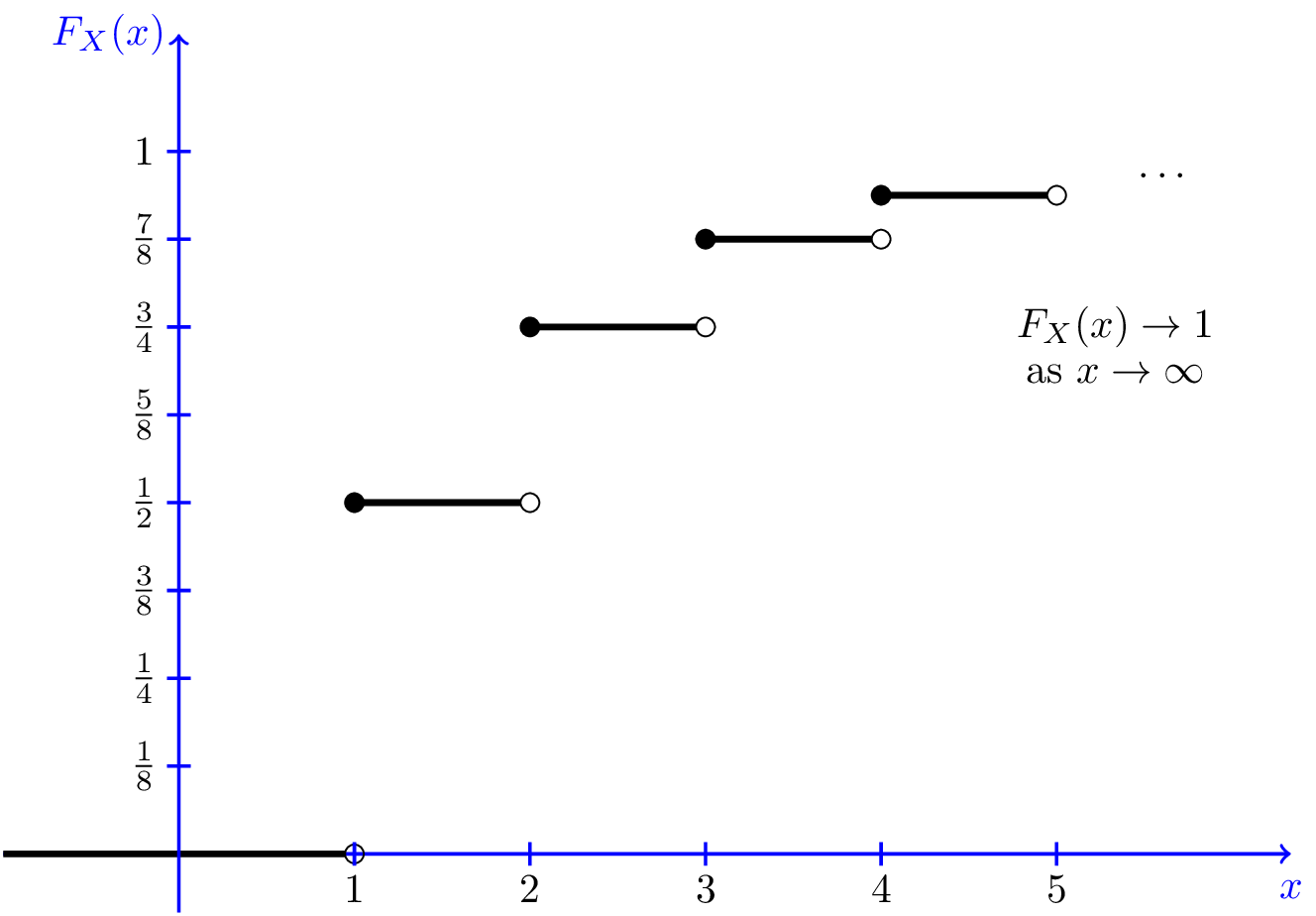
Fig.3.5 - CDF of random variable given in Example 3.10. - To find $P(2 < X \leq 5)$, we can write $$P(2 < X \leq 5)=F_X(5)-F_X(2)=\frac{31}{32}-\frac{3}{4}=\frac{7}{32}.$$ Or equivalently, we can write $$P(2 < X \leq 5)=P_X(3)+P_X(4)+P_X(5)=\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=\frac{7}{32},$$ which gives the same answer.
- To find $P(X > 4)$, we can write $$P(X > 4)=1-P(X \leq 4)=1-F_X(4)=1-\frac{15}{16}=\frac{1}{16}.$$
- To find the CDF, note that
-
First, note that this is a valid PMF. In particular,
$$\sum_{k=1}^{\infty} P_X(k)=\sum_{k=1}^{\infty} \frac{1}{2^k}=1 \textrm{ (geometric sum)}$$

