---

Problem

A coffee shop has $4$ different types of coffee. You can order your coffee in a small, medium, or large cup. You can also choose whether you want to add cream, sugar, or milk (any combination is possible, for example, you can choose to add all three). In how many ways can you order your coffee?

---

Problem

Eight committee members are meeting in a room that has twelve chairs. In how many ways can they sit in the chairs?

---

Problem

There are $20$ black cell phones and $30$ white cell phones in a store. An employee takes $10$ phones at random. Find the probability that

1. there will be exactly $4$ black cell phones among the chosen phones;
2. there will be less than $3$ black cell phones among the chosen phones.

---

Problem

Five cards are dealt from a shuffled deck. What is the probability that the dealt hand contains

1. exactly one ace;
2. at least one ace?

---

Problem

Five cards are dealt from a shuffled deck. What is the probability that the dealt hand contains exactly two aces, given that we know it contains at least one ace?

---

Problem

The 52 cards in a shuffled deck are dealt equally among four players, call them A, B, C, and D. If A and B have exactly $7$ spades, what is the probability that C has exactly $4$ spades?

---

Problem

There are $50$ students in a class and the professor chooses $15$ students at random. What is the probability that you or your friend Joe are among the chosen students?

---

Problem

In how many ways can you arrange the letters in the word "Massachusetts"?

---

Problem

You have a biased coin for which $P(H)=p$. You toss the coin $20$ times. What is the probability that

1. you observe $8$ heads and $12$ tails;
2. you observe more than $8$ heads and more than $8$ tails?

---

Problem

A wireless sensor grid consists of $21 \times 11=231$ sensor nodes that are located at points $(i,j)$ in the plane such that $i \in \{0,1,\cdots,20\}$ and $j \in \{0,1,2,\cdots,10\}$ as shown in Figure 2.1. The sensor node located at point $(0,0)$ needs to send a message to a node located at $(20,10)$. The messages are sent to the destination by going from each sensor to a neighboring sensor located above or to the right. That is, we assume that each node located at point $(i,j)$ will only send messages to the nodes located at $(i+1,j)$ or $(i,j+1)$. How many different paths do exist for sending the message from node $(0,0)$ to node $(20,10)$?

---

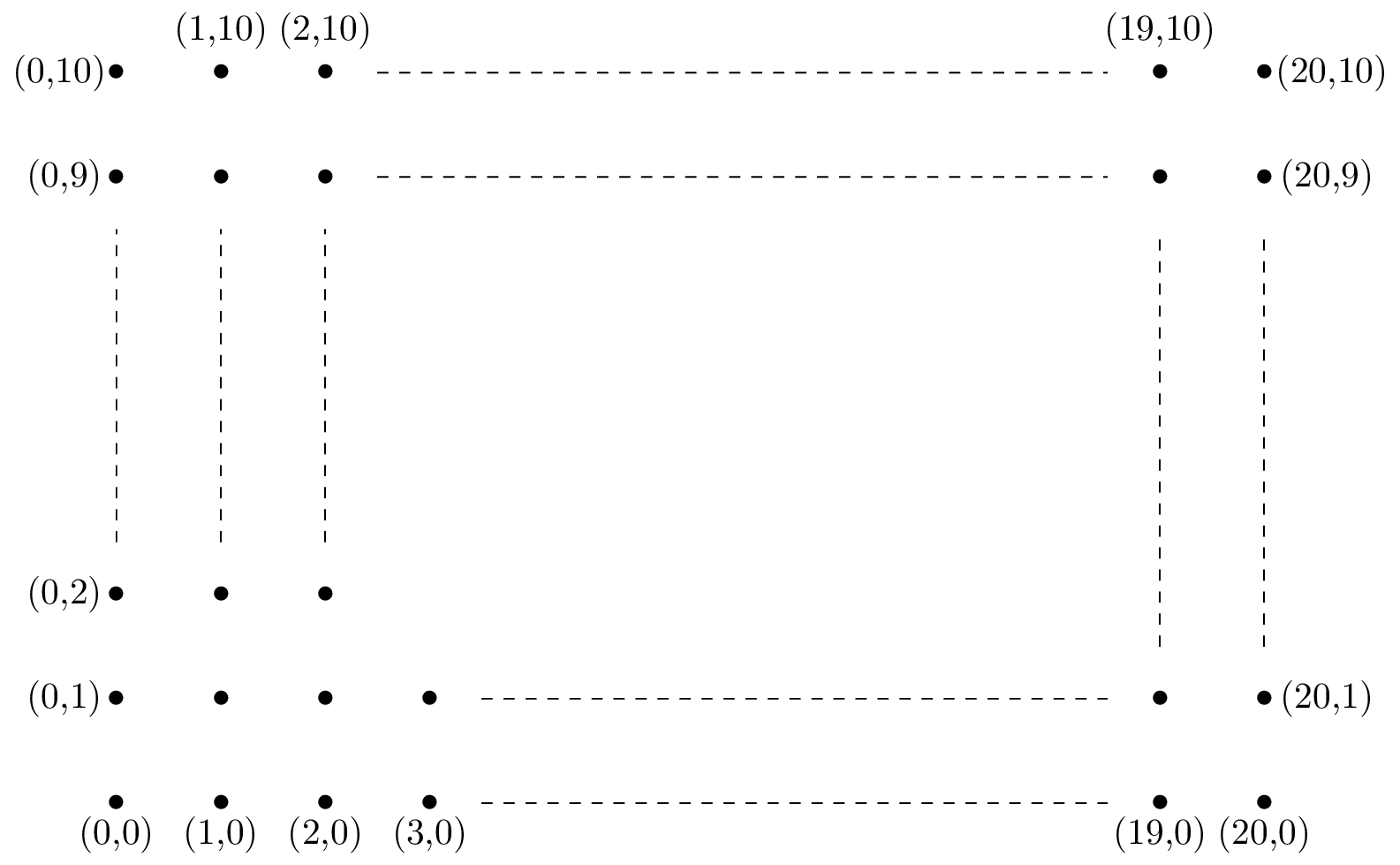
Problem

In Problem 10, assume that all the appropriate paths are equally likely. What is the probability that the sensor located at point $(10,5)$ receives the message? That is, what is the probability that a randomly chosen path from $(0,0)$ to $(20,10)$ goes through the point $(10,5)$?

---

Problem *

In Problem 10, assume that if a sensor has a choice, it will send the message to the above sensor with probability $p_a$, and will send the message to the sensor to the right with probability $p_r=1-p_a$, (independently from other sensors). What is the probability that the sensor located at point $(10,5)$ receives the message?

---

Problem

There are two coins in a bag. For Coin 1, $P(H)=\frac{1}{2}$ and for Coin 2, $P(H)=\frac{1}{3}$. Your friend chooses one of the coins at random and tosses it 5 times.

1. What is the probability of observing at least $3$ heads?
2. * You ask your friend: "Did you observe at least three heads?". Your friend replies, "Yes." What is the probability that Coin 2 had been chosen?

---

Problem

There are 15 people in a party, including Hannah and Sarah. We divide the 15 people into 3 groups, where each group has 5 people. What is the probability that Hannah and Sarah are in the same group?

---

Problem

You roll a die $5$ times. What is the probability that at least one value is observed more than once?

---

Problem

I have 10 red and 10 blue cards. I shuffle the cards and then label the cards based on their orders: I write the number one on the first card, the number two on the second card, and so on. What is the probability that

1. All red cards are assigned numbers less than or equal to $15$?
2. Exactly $8$ red cards are assigned numbers less than or equal to $15$?

---

Problem

I have two bags. Bag 1 contains $10$ blue marbles, while Bag 2 contains $15$ blue marbles. I pick one of the bags at random, and throw $6$ red marbles in it. Then I shake the bag and choose $5$ marbles (without replacement) at random from the bag. If there are exactly $2$ red marbles among the $5$ chosen marbles, what is the probability that I have chosen Bag 1?

---

Problem

In a communication system, packets are transmitted from a sender to a receiver. Each packet is received with no error with probability $p$ independently from other packets (with probability $1-p$ the packet is lost). The receiver can decode the message as soon as it receives $k$ packets with no error. Find the probability that the sender sends exactly $n$ packets until the receiver can decode the message successfully.

---

Problem

How many distinct solutions does the following equation have such that all $x_i\in \mathbb{N}$? $$x_1+x_2+x_3+x_4+x_5=100$$

---

Problem

How many distinct solutions does the following equation have? $$x_1+x_2+x_3+x_4=100, \textrm{ such that }$$ $$x_1 \in \{0,1,2,\cdots, 10\}, x_2,x_3,x_4 \in \{0,1,2,3,...\}.$$

---

Problem *

For this problem suppose that the $x_i$'s must be non-negative integers, i.e., $x_i\in \{0,1,2,\cdots \}$ for $i=1,2,3$. How many distinct solutions does the following equation have such that at least one of the $x_i$'s is larger than $40$? $$x_1+x_2+x_3=100$$